9) Operaciones con matrices.
A ver si repaso estas operaciones que ya se me olvidaron jejeje.

explorer escribiste:Por favor, creating021, entra en el enlace que he puesto a la página de Wikipedia. Y presta especial atención al gráfico animado de la derecha.creating021 escribiste:Cuando usas esa formula estás encontrando el área de un cuadrilátero regular y dividiéndolo por dos... si el triángulo no es de 90º no puedes usar la fórmula (sin partir el triángulo)... es más, ni siquiera la fórmula de Herón es válida para todos los triángulos (ver geometría hiperbólica y curvatura del espacio-tiempo) aunque con ingenio y mucho tiempo de trabajo se puede lograr.
He revisado media docena de páginas más, de matemáticas, y todas ponen lo mismo. Se puede aplicar la formula independientemente de si es o no un triángulo rectángulo. Nada de partir el triángulo. Si se dispone de una base y de una altura, es fácil calcular su área.
¿Tienes un contraejemplo?
http://descartes.cnice.mecd.es/3_eso/Fi ... ugeo_2.htm
http://www.dmae.upct.es/~pepemar/triangulo/area.htm (el primer applet es particularmente divertido)
http://mimosa.cnice.mecd.es/clobo/geoweb/area5.htm (último applet, todas las combinaciones de base y altura)

explorer escribiste:Como ejercicios para el futuro, estaría bien reescribir estos programas, pero intentando reducirlos a la mitad, a la tercera y a la cuarta parte (o menos).

creating021 escribiste:explorer escribiste:¿Tienes un contraejemplo?
Si... supongamos que tienes un triángulo isósceles, 10 cm. los lados mayores y 5 el menor.
Encuentra el área _sin_ usar pitágoras y usando la fórmula propuesta (b*a/2) de este triángulo (10 cm. los mayores y 5 el menor).
creating021 escribiste:Como verás, en el mismo dibujo animado que comentas, parten el triángulo (de forma imaginaria) en dos (a la mitad) llamándola altura y encontrándola por medio del teorema de pitágoras (ya que forma dos triángulos rectos)... después duplican el área triangular original formando un cuadrilátero regular (base x altura) y lo dividen para tener el triángulo.
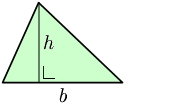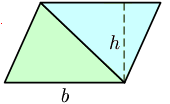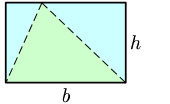

No hay fórmula de pitágoras. Lo que hacen es: dividen el triángulo en dos partes (distintas). Pero en la siguiente secuencia lo que hacen es duplicar la superficie del triángulo y colocar sobre uno de los lados, formando un paralelepípedo (cuya superficie es S=base*altura). De este segundo triángulo lo dividen por la altura, esta vez sí, y "mueven" la parte del triángulo más a la derecha a la parte izquierda del paralelepípedo, para convertirlo en un rectángulo (así es como se demuestra el cálculo de la superficie de un paralelepípedo). Bueno, pues si la superficie de este rectángulo es base por altura, como hemos duplicado el área del triangulo original, significa que su área es la mitad.

a= 2
b= 7
c= 500
Zeokat escribiste:La formula de Herón me parece que tiene unas limitaciones, esta claro que es la forma más sencilla. Pero creo recordar que en triángulos con forma de alfiler esta fórmula falla. El caso de triángulo con forma de alfiler se da si introduces dimensiones para dos de los lados pequeñas en relación al otro lado, por ejemplo:
- Código: Seleccionar todo
a= 2
b= 7
c= 500

Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 0 invitados